§2.3. FRECVENTALISMUL
Se știe că, încă de la începutul teoriei probabilităților
au fost două căi de a aborda teoria: prima, cea studiată în §2.1, a probabilităților apriori, date prin considerente de simetrie se baza pe supoziția egal posibilului. Cealaltă, a cărei istorie merge până la Huygens
și Jean de Witt, provine din statistică. Ea se bazează pe probabilitățile aposteriori:
ca să estimezi probabilitatea apariției lui 6 la un zar adevărat, nu poți
face altfel decât să arunci zarul de un număr foarte mare de ori. În secolul
XIX, prima metodă a avut cea mai mare autoritate datorită contribuției decisive
a lui Laplace.
Dar, unul
din punctele slabe ale definiției lui Laplace a fost cercul vicios dat de expresia
egal posibil și de a pretinde apoi că a dat o definiție bună. Cournot (1843),
C. Boole (1854), J. Venn (1866) au întrebat cum este posibil să dovedești că
un zar nu este falsificat altfel decât aruncându-l de un număr mare de ori ?
De aceea, J. Venn a fost primul care a îcercat să inverseze ordinea, definind
probabilitatea în termeni de frecvență relativă ([63], 1866). A apărut o dificultate de următorul gen: ca să definim
probabilitatea ca limită a frecvenței relative, trebuie să ne restrângem la
șirurile (de 0 și 1 pentru simplitate) care au proprietatea că 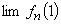 există,
unde
există,
unde 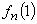 este
frecvența relativă a apariției unui 1 în primii n termeni ai șirului
rezultatelor experimentului. Dar nu toate șirurile de acest fel sunt bune. Nimeni
nu va pretinde că dacă la o aruncare cu banul apare șirul 00110011001100110011....
aruncarea a fost cinstită, deși limita frecvenței relative (sau limita Venn,
cum se mai numește) există și este egală cu
este
frecvența relativă a apariției unui 1 în primii n termeni ai șirului
rezultatelor experimentului. Dar nu toate șirurile de acest fel sunt bune. Nimeni
nu va pretinde că dacă la o aruncare cu banul apare șirul 00110011001100110011....
aruncarea a fost cinstită, deși limita frecvenței relative (sau limita Venn,
cum se mai numește) există și este egală cu 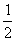 . Ar trebui
studiate numai șiruri aleatoare, care corespund unor aruncări reale. El nu
a putut rezolva problema definirii obiectelor de care avea nevoie.
. Ar trebui
studiate numai șiruri aleatoare, care corespund unor aruncări reale. El nu
a putut rezolva problema definirii obiectelor de care avea nevoie.
Într-o lucrare foarte interesantă
([63], 1888) Venn critică interpretarea subiectivistă extremistă
a noțiunii de probablitate, arătând că, deși probabilitatea are și o latură
subiectivă, ea este derivată din considerente de frecvențe (de obicei). De Morgan
(1847) considera probabilitatea soră a logicii, care ar trebui să studieze gradul
de încredere al inferenței din premise față de care exită o încredere parțială.
Iar Donkin (1851) considera evident că obiectul teoriei probabilităților este
cantitatea de încredere (quantitz of belief). Venn arată că gradul de încredere
în ceva nu este un concept cu care să poată lucra știința deoarece variază de
la individ la individ, și chiar la același individ în perioade de timp diferite.
În plus, nu este măsurabil; chiar dacă ar fi măsurabil, studierea lui ar fi
de domeniul psihologiei. Făcând paralela cu logica, probabilitatea nu este gradul
de încredere al fiecăruia, ci gradul de încredere pe care ar trebui să îl aibă
o persoană rațională față de o anumită propoziție; iar dacă aprofundăm, o persoană
rațională ar trebui să aibă un nivel de încredere în ceva egal cu probabilitatea
lui obiectivă. La oamenii concreți, nivelul de încredere nu este dat numai de
frecvența statistică, ci și de alții care pentru o teorie riguroasă nu sunt
relevanți: Nu are rost să spunem ce cred oamenii, noi vrem să știm ce au dreptate
să creadă; iar aceasta nu se va putea tranșa fără a apela la fenomenele însăși
([63], §14). De aceea, partea subiectivă a probabilității,
deși foarte interesantă... pare un simplu apendice al celei obiective, care
nu are o bază solidă. Întotdeauna când un om rațional pariază 5 contra 1 că
nu va cădea 6 la o aruncare cu zarul, nu deoarece 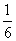 este
convins că va cădea 6 și
este
convins că va cădea 6 și 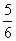 este
convins de contrariu, ci deoarece el știe că în serii lungi de aruncări 6
va apărea aproximativ într-o șesime din cazuri. Ce are a face acest lucru cu
un pariu la o singură aruncare contingentă ? Aceasta nu este decât traducerea
în practică a convingerii noastre asupra a ceea ce se petrece în serii mari
de aruncări răspunde Venn ([63],
§22). Pur și simplu este vorba
de o translatare a regulii care este justificată la serii lungi în cazul unui
singur pariu. Este un lucru relativ și depinzând de punctul de vedere al evenimentului
izolat sau al colectivului. Iată un alte exemplu ([63], §25): Știu că voi muri în una din cele 7 zile
ale săptămânii. Credința mea că voi muri într-o duminică este, deci,
este
convins de contrariu, ci deoarece el știe că în serii lungi de aruncări 6
va apărea aproximativ într-o șesime din cazuri. Ce are a face acest lucru cu
un pariu la o singură aruncare contingentă ? Aceasta nu este decât traducerea
în practică a convingerii noastre asupra a ceea ce se petrece în serii mari
de aruncări răspunde Venn ([63],
§22). Pur și simplu este vorba
de o translatare a regulii care este justificată la serii lungi în cazul unui
singur pariu. Este un lucru relativ și depinzând de punctul de vedere al evenimentului
izolat sau al colectivului. Iată un alte exemplu ([63], §25): Știu că voi muri în una din cele 7 zile
ale săptămânii. Credința mea că voi muri într-o duminică este, deci, 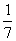 . Evenimentul
nu admite, în mod evident nici o repetare; totuși, nu credem cu toții la fel
?... Este adevărat că nu pot muri decât o dată, dar aparțin unei clase în care
moartea apare frecvent și opinia mea se formează după experiența acestei clase.
Dacă mi-aș asigura viața pentru 1000 lire, aș considera corect să cer 7000 dacă
societatea declară că nu va plăti decât decesele duminicale. Din puctul meu
de vedere, poate că nu ar fi prea echitabil, dar dacă toți ar fi asigurați confoem
acestui principiu, pentru societatea de asigurați conform acestui principiu,
pentru societatea de asigurări nu ar fi nici o diferență.
. Evenimentul
nu admite, în mod evident nici o repetare; totuși, nu credem cu toții la fel
?... Este adevărat că nu pot muri decât o dată, dar aparțin unei clase în care
moartea apare frecvent și opinia mea se formează după experiența acestei clase.
Dacă mi-aș asigura viața pentru 1000 lire, aș considera corect să cer 7000 dacă
societatea declară că nu va plăti decât decesele duminicale. Din puctul meu
de vedere, poate că nu ar fi prea echitabil, dar dacă toți ar fi asigurați confoem
acestui principiu, pentru societatea de asigurați conform acestui principiu,
pentru societatea de asigurări nu ar fi nici o diferență.
Cel care
a făcut încercarea temerară de a construi o teorie a probabilităților pe baze
frecvențialiste a fost von Mises (1892 - 1953). Importanța teoriei, creată de
el este foarte mare prin lupta de idei pe care a generat-o privind atât modelarea
matematică a conceptului de probabilitate cât și interpretarea lui epistemologică.
Astăzi, matematicienii nu mai folosesc, în general, formalizarea lui, deși încă
mai există susținători ai unor neofrecvențialisme mai sofisticate (Salmon,
Connover).
Din 1919
când a apărut prima versiune a lucrării fundamentale Grundlagen der Wahrscheinlichkeitsrechnung,
von Mises nu a încetat să își perfecționeze teoria ajungând ca ediția [38], apărută post mortem, să conțină aproape 700
de pagini. La fundamentarea matematică riguroasă a frecvențialismului a contribuit
aproape exclusiv școala germană de probabilități: K. Dörge ([49], 1932), E. Tornier ([49],
1933), E. Kamke ([49], 1932) și, mai ales marele statistician A. Wald ([49], 1937 și [38], 1947).
Școlile
de matematică franceză, anglo-saxonă, sovietică au respins de la bun început
frecvențialismul. Pentru primii, teoria este oribilă matematic; pentru subiectiviștii
englezi, conceptul de probabilitate obiectivă, asimpototică, limită a frecvențelor
era respins ca nerelevant empiric și insuficient în aplicații.
Noi vom
studia teoria așa cum apare în [38]
care este cea mai elaborată formal, matematic.
Von Mises
a fost primul care a trasat o linie de demarcație clară între teoria matematică
a probabilităților și problema aplicării teoriei. Deoarece prima sarcină a
oricărui demers științific este limitarea scopului, noi ne vom limita la elaborarea
unei teorii a evenimentelor repetabile. Se precizează clar nu avem în vedere
probleme ca care este probabilitatea ca Iliada și Odiseea să aibă același
autor sau estimarea probabilității de adevăr a legendelor biblice și nici
măcar nu știm să dăm un sens unei întrebări ca: Care este probabilitatea ca
Anglia să intre în război cu Egiptul . Ceea ce are în vedere, în schimb, este
introducerea unui concept matematic care să aibă aceeași structură cu celelalte
concepte fundamentale din orice domeniu unde se folosește modelarea matematică.
Teoria probabilităților nu este și nu trebuie să fie, susține von Mises, matematică
pură. Ea trebuie să fie o disciplină matematizată, așa ca mecanica, dar nu un
domeniu al matematicii ca algebra sau analiza. (Punctul acesta de vedere teoria
probabilităților ca o știință a naturii este respins astăzi in corpore de
matematicieni. Nu este nici o problemă neclară privind probabilitatea se
aude foarte des din lumea noastră matematică. Ea este o măsură cu masa totală
egală cu 1 Mai mult, este refuzat chiar dreptul la existență al teoriei;
teoria probabilităților ar fi un subdomeniu al teoriei măsurii. Bourbaki nu
a scris nici un tratat de probabilități.) Consider că din punct de vedere epistemologic
poziția lui von Mises este corectă și responsabilă. Paralela cu mecanica mi
se pare relevantă.
Modelul
avut în vedere de el în deifiniția probabilității a fost viteza din mecanica
clasică. Ea este definită printr-o limită 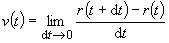 . Probabilitatea
se definește relativ la un colectiv prin limita frecvențelor
relative când n, numărul probelor, tinde la infinit. Nu are sens să ne
întrebăm dacă aceste limite există continuă el deoarece teoria pleacă exact
de la această supoziție. Fără viteză nu ar fi posibilă mecanica. Dacă viteza
există în realitate, nimeni nu poate ști sau verifica. Poate că mai degrabă
nu există și modelarea mișcării prin continuum nu este corectă. Dar, dacă noțiunea
de viteză nu ridică obiecții, de ce ar fi ele ridicate de noțiunea de probabilitate
ca limită a frecvențelor ?
. Probabilitatea
se definește relativ la un colectiv prin limita frecvențelor
relative când n, numărul probelor, tinde la infinit. Nu are sens să ne
întrebăm dacă aceste limite există continuă el deoarece teoria pleacă exact
de la această supoziție. Fără viteză nu ar fi posibilă mecanica. Dacă viteza
există în realitate, nimeni nu poate ști sau verifica. Poate că mai degrabă
nu există și modelarea mișcării prin continuum nu este corectă. Dar, dacă noțiunea
de viteză nu ridică obiecții, de ce ar fi ele ridicate de noțiunea de probabilitate
ca limită a frecvențelor ?
Conceptul
de bază al teoriei lui von Mises este cel de colectiv. Dacă S este o
mulțime oarecare de etichete (label), șirul 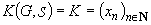 se numește
colectiv dacă: S este o familie de părți din S (corp de mulțimi);
G este o familie de place selections închisă la anumite operații grupale;
pentru orice mulțime
se numește
colectiv dacă: S este o familie de părți din S (corp de mulțimi);
G este o familie de place selections închisă la anumite operații grupale;
pentru orice mulțime  S
limita șirului
S
limita șirului  există
și se notează cu
există
și se notează cu 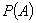 , unde
, unde
 este
frecvența termenilor din șirul K aparținând mulțimii A:
este
frecvența termenilor din șirul K aparținând mulțimii A:
 ; orice
place selection,
; orice
place selection, 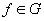 produce
un nou colectiv K cu proprietatea de convergență
anterioară. Wald [62] a demonstrat consistența noțiunii.
produce
un nou colectiv K cu proprietatea de convergență
anterioară. Wald [62] a demonstrat consistența noțiunii.
După Mises,
probabilitatea nu are sens decât dacă se specifică un colectiv de evenimente
în care evenimentul a cărui probabilitate se caută apare cu o anumită fercvență.
Sarcina teoriei probabilităților este de a calcula repartiții de probabilități
în colective derivate din repartițiile date în colectivele inițiale. Apare
însă o problemă: aceluiași eveniment i se pot circumscrie mai multe probabilități,
depinzând de colectivul în care este gândit. De exemplu: P(x moare mâine)
este una dacă îl gândesc pe x ca făcând parte din categoria cetățenilor
de 42 de ani, alta dacă se referă la cei între 40-45 ani, alta dacă se referă
la bărbați de 42 de ani, etc. În exemplul acesta dat de von Mises ([??], pag.13) este deja ceva neriguros: un colectiv se presupune
infinit, iar numărul cetățenilor unui stat este finit. Mises comnetează în aceeași
pagină: aici aplicăm teoria la o populație mare, dar finită. Or, la o populație
finită nu mai este nici o teorie de aplicat căci axioma limitei își pierde sensul;
probabilitățile devin frecvențe relative care sunt variabile. Iar apropos de
mare, Good remarca pe bună dreptate ([20]): Mises a spus că șirurile trebuie să fie lungi (ca
să merite denumirea de colectiv) dar nu a spus cât de lungi, la fel ca un geometru
care spune că punctele trebuie să fie mici pentru a se numi puncte, fără să
spună cât de mici. Statisticianul este ca un desenator cu un creion bont: el
vrea să știe cât de lung trebuie să fie șirul. Keynes, comentând la rândul
lui definiția frecvențialistă a probabilității prin long run frequency, scria
[20] că In long run we shall be all dead.
Apoi s-a
reproșat că ceea ce se întâmplă la limită nu are nici o relevanță pentru estimarea
probabilității unui eveniment contingent: că, de exemplu, un șir absurd de tipul
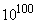 de 1 și
apoi 0 este permis în teoria sa ca un colectiv bine definit cu
de 1 și
apoi 0 este permis în teoria sa ca un colectiv bine definit cu  ,
,
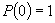 , față
de orice place selection; că în fizică am dori ca
, față
de orice place selection; că în fizică am dori ca 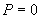 să însemne
imposibilitate fizică, iar dacă un fenomen apare de
să însemne
imposibilitate fizică, iar dacă un fenomen apare de  ori,
el este mai necesar fizic decât rotația pământului în jurul soarelui; nu vor
f, cu siguranță, mai mult de
ori,
el este mai necesar fizic decât rotația pământului în jurul soarelui; nu vor
f, cu siguranță, mai mult de  rotații
ale pământului în jurul axei sale până la dispariția sistemului solar. (Vârsta
universului este apreciată la cu mult mai puțin de
rotații
ale pământului în jurul axei sale până la dispariția sistemului solar. (Vârsta
universului este apreciată la cu mult mai puțin de 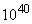 secunde
!)
secunde
!)
Mises
a sesizat că, în unele cazuri probabilitatea sa este o măsură pe o anumită algebră,
dar a considerat faptul neesențăal. Pentru el, abordarea measuristă (Kolmogorov,
etc) nu este satisfăcătoare deoarece nu numai probabilitatea ci și masa, sarcina
electrică. ???? Este adevărat că este foarte comod din punct de vedere matematic
să folosești o teorie gata făcută, dar aceasta este numai o abordare parțială.
Se constată în teoria probabilităților spune Mises - tendința de a lucra
partea matematică foarte riguros, fără a se manifesta interes suficient asupra
a ceea ce este mai important: tratarea teoriei probabilităților ca o știință
în sine, nu ca un subdomeniu al teoriei măsurii.
Cramér
i-a reproșat în [11] că definiția lui von Mises este o mixtură de
empiric și teoretic, de obicei evitată în știința matematică modernă. Este ca
și cum ai defini punctul ca fiind limita unui șir de pete de cretă din ce în
ce mai mici pe o tablă neagră. Răspunzând, Mises că mixtura de elemente teoretice
și empirice este de neînlăturat în orice teorie matematică. În teoria elasticității
se introduc tensiuni și stressuri care, din punct de vedere matematic sunt tensori
de ordin II. Totuși, teoria elasticității nu este analiză tensorială. Dar observația
lui Cramér conține și ceva adevărat: trecerea de la observație la modelarea
matematică nu poate fi complet matematizată, nu este o concluzie logică, ci
mai degrabă o problemă de alegere([38], pag. 32).
Mises
polemizează cu Kolmogorov mai ales în ceea ce privește definiția conceptului
de independență. Pentru primul, nu se poate vorbi de evenimente independente,
ci despre colective independente. Pentru ultimul, este o ipoteză privind probabilitatea
conjuncției a două evenimente (sau, mai general, a două  - algebre
de evenimente: A este independent de B dacă
- algebre
de evenimente: A este independent de B dacă  ). Definiția
lui Kolmogorov a independenței pare mai degrabă o generalizare a unui concept
care are sens. Ea duce la inferențe care au foarte puțin de a face cu
semnificația general acceptată a termenului pe care se presupune că o reproduce.
([38], §1.10).
). Definiția
lui Kolmogorov a independenței pare mai degrabă o generalizare a unui concept
care are sens. Ea duce la inferențe care au foarte puțin de a face cu
semnificația general acceptată a termenului pe care se presupune că o reproduce.
([38], §1.10).
În Anexa
2 din lucrarea citată, Mises rezumă foarte clar punctul său de vedere astfel:
a)
teoria este frecevnțialistă;
b)
orice afirmație despre probabilitatea unui eveniment trebuie să fie, măcar pricipial
verificabilă;
c)
pentru measuriști frecvența nu este decât ceva derivat, neesențial (afterthought).
Din păcate,
deși el încearcă să facă din teoria probabilităților o teorie aplicată, ceva
de mijloc între consumatorul de statistică, căutând rețete, formule gata făcute
și puriștii pentru care probabilitatea este o ramură a teoriei măsurii sau o
măsură pe algebre Boole și care resping frecvența ca fiind groaznică matematic
(Anexa 2 din [38]), teoria lui a căzut mai ales din greutățile
conceptuale formidabile în aplicarea ei. Kolmogorov arăta (citat din [31], pag.23) că: ipoteza caracterului probabilistic
al experiențelor, adică ipoteza că frecvențele au tendința de a se grupa în
jurul unui număr constant este corectă ca atare... numai dacă se păstrează anumite
condiții care nu se pot menține un timp nelimitat și cu o precizie nelimitată.
De aceea, trecerea exactă la limită  nu poate
avea o semnificație reală. Enunțarea principiului stabilității frecvențelor
prin folosirea unei asemenea treceri la limită cere difinirea modurilor admise
de găsire a șirurilor infinite de experiențe care, iarăși nu poate fi decât
o ficțiune matematică. Toată această acumulare de noțiuni ar merita să fie supusă
unei analize serioase numai dacă s-ar obține ca rezultat construcția unei teorii
atât de specifice, încât fundamentarea ei riguroasă să se dovedească imposibilă
pe alte căi.
nu poate
avea o semnificație reală. Enunțarea principiului stabilității frecvențelor
prin folosirea unei asemenea treceri la limită cere difinirea modurilor admise
de găsire a șirurilor infinite de experiențe care, iarăși nu poate fi decât
o ficțiune matematică. Toată această acumulare de noțiuni ar merita să fie supusă
unei analize serioase numai dacă s-ar obține ca rezultat construcția unei teorii
atât de specifice, încât fundamentarea ei riguroasă să se dovedească imposibilă
pe alte căi.
Pentru
O. Onicescu [41], teoria lui von Mises merită să fie păstrată,
dar nu atât ca o teorie a probabilităților, cât ca una a colectivelor statistice.
În alt loc ([42], pag.439) consideră metoda sa ca fiind
uneori acceptabilă pentru a trece de la frecvențe la probabilități: Știm pentru
multe experimente cum să trecem de la frecvențe la probabilități și să conferim
ultimelor caracterul (indubitabil) existențial al primelor. Dar de fiecare dată
trebuie să știm obiectul a cărui existență este asertată de probabilitate. În
cazul urnei, acest obiect este chiar structura ei.
Teoria lui von Mises a
sugerat acest procedeu pentru orice domeniu unde experimentele efectuate asupra
unor colective stabile ar fi trebuit să reveleze prin frecvențele apărute, structura
lor subiacentă
Modelul său este satisfăcător pentru o largă clasă de mulțimi
statistice cărora reușește să le confere probabilități.
Argumente
metodologice asemănătoare cu acelea ale lui Kolmogorov aduc și P. Suppes (1970):
fundamentarea statisticii pe baze frecvențialiste este prohibitiv de complicată.
În plus, teoria, deși se consideră obiectivistă, dă dovadă de un mare grad de
arbitrar în tratarea problemei evenimentului aleator unic, anume în fixarea
clasei de referință pentru acel eveniment.
Un alt
reprezentant de frunte al frecevnțialismului este H. Reichenbach, mai
ales în cartea sa [49], 1935. Teoria lui von Mises completată de Reichenbach
l-a influențat pe von Neumann în axiomatizarea mecanicii cuantice. Cartea [49]
este, probabil, cea mai riguroasă din punct de vedere filosofic; din păcate
nu și matematic. Aici este prezentată și logica probabilistă a lui Reichenbach,
care a fost mult discutată. Pentru el, propoziția  este
o implicație de un tip sui generis, o aserțiune privind apartenența unor obiecte
la o clasă. Toate probabilitățile sunt condiționate.
este
o implicație de un tip sui generis, o aserțiune privind apartenența unor obiecte
la o clasă. Toate probabilitățile sunt condiționate.  înseamnă
de fapt
înseamnă
de fapt 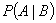 , unde
B se subînțelege.
, unde
B se subînțelege.
Reichenbach
a încercat să îl corecteze pe von Mises din două puncte de vedere. În primul
rând, conceptul fundamental este de probabilitate condiționată 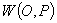 ; în al
doilea, a renunțat la ipoteza hazardului (regellosigkeit) ca fiind de nesusținut
logic.
; în al
doilea, a renunțat la ipoteza hazardului (regellosigkeit) ca fiind de nesusținut
logic.
Din punct
de vedere formal, structura unei aserțiuni probabilistice este aceea a unei
implicații generale privind aparteneța elementelor la clase (pag.37). Conceptul
central este implicația probabilistă notată  . Propoziția
. Propoziția
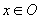
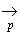
 se citește
se citește
 implică
probabilistoc de grad p că
implică
probabilistoc de grad p că  . În
știință, x se poate gândi ca premiză, cauză, condiție, context experimental,
iar y ca rezultat, efect. Notația prescurtată a propoziției de mai sus
este
. În
știință, x se poate gândi ca premiză, cauză, condiție, context experimental,
iar y ca rezultat, efect. Notația prescurtată a propoziției de mai sus
este 
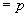 .
.
Studiul
logic al implicației probabiliste îl duce la o axiomatizare a calculului probabilităților
mai generală decât a lui Kolmogorov (pentru că se referă la probabilitatea condiționată,
pentru că este numai aditivă și nu  -aditivă
și, în sfârșit pentru că nu este legată de o viziune ansamblistă ca axiomatizarea
lui Kolomogorov) dar care nu a fost adoptată de matematicieni (tocmai pentru
că era prea generală) ci numai de logicieni și filosofi. Sistemul său axiomatic
a apărut cu un an înaintea celui kolmogorovian (Ayiomatic der Wahrscheinlichkeitsrechnung,
Math. Zs., 34, 568 619, 1932). El este prezentat în Anexa 4.
-aditivă
și, în sfârșit pentru că nu este legată de o viziune ansamblistă ca axiomatizarea
lui Kolomogorov) dar care nu a fost adoptată de matematicieni (tocmai pentru
că era prea generală) ci numai de logicieni și filosofi. Sistemul său axiomatic
a apărut cu un an înaintea celui kolmogorovian (Ayiomatic der Wahrscheinlichkeitsrechnung,
Math. Zs., 34, 568 619, 1932). El este prezentat în Anexa 4.
Ca epistemolog,
Reichenbach nu putea fi mulțumit cu prezentarea unui sistem axiomatic. Crearea
lui este numai un prim pas în lămurirea problemei. Mai importantă este interpretarea
lui intensivă (inhaltliche) căci este foarte greu de înțeles semnificația legilor
calculului probabilităților fără o interpretare intensivă a conceptului de probabilitate
(pag. 80). Din mulțimea interepretărilor posibile, se decelează două mai importante:
- Interpretarea
frecvențială. Probabilitatea este limita frecvențelor parțiale, dacă aceasta
există: 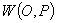
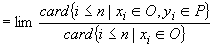 . Această
interepretare îl duce la un sistem axiomatic mai particular, o relaizare a celui
general în lumea șirurilor. Șirurile tip pentru care are sens să se vorbească
de probabilitate în interpretarea ei ca limită, le numește perechi normale de
șiruri, sau șiruri normale (cuvântul este luat de Borel, 1925, care îl folosea
în alt sens). Șirurile normale sunt o condiție mai slabă decât regellosigkeit-ul
lui von Mises. În principiu, lor nu li se cere decât să fie libere de influența
predecesorului și, dacă sunt împărțite în k subșiruri, numărând din k
în k, fiecare din subșirurile obținute să fie libere de influența predecesorilor. Definiția șirurilor
normale este și mai complicată decât axioma hazardului a lui Mises; în plus,
tratarea matematică este imposibilă pentru un matematician care are bunăvoința
să încerce să priceapă despre ce este vorba.
. Această
interepretare îl duce la un sistem axiomatic mai particular, o relaizare a celui
general în lumea șirurilor. Șirurile tip pentru care are sens să se vorbească
de probabilitate în interpretarea ei ca limită, le numește perechi normale de
șiruri, sau șiruri normale (cuvântul este luat de Borel, 1925, care îl folosea
în alt sens). Șirurile normale sunt o condiție mai slabă decât regellosigkeit-ul
lui von Mises. În principiu, lor nu li se cere decât să fie libere de influența
predecesorului și, dacă sunt împărțite în k subșiruri, numărând din k
în k, fiecare din subșirurile obținute să fie libere de influența predecesorilor. Definiția șirurilor
normale este și mai complicată decât axioma hazardului a lui Mises; în plus,
tratarea matematică este imposibilă pentru un matematician care are bunăvoința
să încerce să priceapă despre ce este vorba.
Interpretarea
geometrică (astăzi am spune asamblistă):
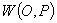
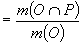 , unde
m este o măsură finit aditivă pe un corp de părți ale unei mulțimi generale
E. La kolmogorov se cere ca măsura să fie
, unde
m este o măsură finit aditivă pe un corp de părți ale unei mulțimi generale
E. La kolmogorov se cere ca măsura să fie
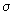 -aditivă,
deci o condiție mai tare.
-aditivă,
deci o condiție mai tare.
Dacă din
punct de vedere teoretic, matematic, oricare din cele două interpretări este
la fel de justificată, nu la fel stau lucrurile din punct de vedere al aplicării
teoriei, subliniază autorul. Trebuie să ne întrebăm care interpretare este
implicată când se fac aserțiuni probabuilistice în știință sau viața de zi cu
zi (pag. 326). Iar această interpretare i se pare neapărat cea frecvențială
care, astfel, ar fi primară din punct de vedere logic. Nu pot exista dubii
că aceasta este cea frecvențială. Când se zice că probabilitatea de a lovi o
țintă este p ... se înțelege o asertare de frecvență, nu geometrică.
Se poate argumenta că probabilitatea de lovire a țintei este dată de un raport
între două măsuri, dar, din punct de vedere geometric este absolut indiferent
cum se alege măsura ariei țintei... În aplicarea teoriei la experimente practice
funcția de densitate nu mai este arbitrară, ci trebuie aleasă ca să se potrivească
cu frecvențele observate... Interpretarea frecvențialistă este logic primară
și conține semnificația reală a conceptului de probabilitate iar cea geometrică
este numai o reprezentare analitică a raporturilor între frecvențe. Izomorfismul
probabilitate măsură nu trebuie considerat identitate.
Criticând
interpretarea subiectivistă (Keynes, 1921) conform căreia probablitatea este
o estimare a gradului de încredere atașat unei propoziții, reichenbach arată
că abordarea probabilității prin prisma evenimentului aleator unic este greșită:
probabilitatea se referă numai la șiruri de evenimente. De fiecare dată când
se vorbesște de probabilitatea unui eveniment, se are în vedere tacit o clasă
de referință. De exemplu probabilitatea ca mâine să plouă interpretată ad
literam, nu are nici un sens. Dar nu trebuie să ne lăsăm induși în eroare de
imprecizia limbajului obișnuit. Din contră, prima sarcină a unui demers filosofic
este să facă riguroasă exprimarea (pag. 328); se poate atașa un sens obiectiv
probabilității respective dacă de referim la anotimp, la presiunea atmosferică,
nebulozitate, etc, așa cum se procedează la birourile meteorologice. Dacă, totuși,
un marinar poate estima mai bine timpul probabil decât un institut meteorologic
situat la sute de kilometri distanță, aceasta nu schimbă situația că, principial
problemele sunt statistice. De vină este, pur și simplu faptul că nu putem avea
statistici suficiente pentru toate previziunile de care avem nevoie.
În epistemologia
lui reichenbach, conceptul de probabilitate joacă un rol central. Din moment
ce toate cunoștințele noastre sunt probabile, când nici o lege a naturii nu
se referă la natură, ci este o idealizare obținută prin neglijarea unei infinități
de factori, când aplicarea oricărei științe la previziunea realului se face
întotdeauna făcând ipoteza unor anumitor raporturi ideale, deși se știe că raporturile
reale nu coincid cu ele, înseamnă că nu se poate rezolva problema cunoașterii
fără a se recunoaște că în aplicarea legilor naturii la realitate nu se obțin
niciodată propoziții sigure, ci numai probabile, deci fără a se lămuri conceptul
de probabilitate. El apare în arenă o dată cu știința; probabilitatea intervine
în cunoașterea naturii numai odată cu asocierea unei structuri ideale realității.
Ipoteza determinismului cauzal ar trebui formulată riguros sub forma probabilitatea
predicției se poate face arbitrar de aproape de 1 (pag. 10). Iar că acesta
nu este cazul întotdeauna, arată relațiile de nedeterminare ale lui Heisenberg
care dau o limtă superioară probabilității predicției. Aceasta înseamnă o formă
mai generală de legitate naturală (pag. 11).
Ceea ce
nu au înțeles filosofii arată el este că nu se poate face o analiză logică
a conceptului de probabilitate decât în legătură cu analiza aceluiași concept
folosit în matematică. Abai aici el capătă o formă riguroasă necesară decelării
structurii sale logice... De-abia un concept decelat suficient de precis se
poate preta la o analiză filosofică riguroasă (pag. 12). De aceea, el speră
să realizeze o construcție mulțumitoare atât logic cât și matematic a calculului
probabilităților și a aplicării acestui calcul la realitate. Sarcina asumată
este de o extraordinară întindere epistemologică. Căci nu este vorba aici de
un concept particular al vreunei discipline înguste, ci de un concept fundamental
în cadrul căruia se petrece cunoașterea naturii și fără clarificarea căruia
nu se poate aștepta o clarificare a problemei cunoașterii. Nu este vorba de
o problemă de matematică sau de fizică matematică, ci de ultimele noastre cunoștințe:
e vorba de întrebarea: ce sens au afirmațiile noastre privind realitatea.
Ste natural
că o lucrare cu asemenea ambiții nu putea să treacă cu vederea problema aplicării
teoriei la realitate, cum este acuzat von Mises și ceilalți matematicieni. Atâta
vreme cât privim Calculul probabilităților ca pe un simplu calcul, în care se
operează numai cu formule, nu există nici o problemă a asertărilor de probabilitate
(a asignării unei probabilități unui eveniment, n.n.). Dar ar fi o dovadă de
miopie dacă am refuza problema ca fiind fără sens (pag. 82). Din moment ce
matematicianul a optat pentru o interpretare intrinsecă (inhaltlich) a conceptului
(fie frecvențialist, fie measurist n.n.) apare și problema: cum se poate decide
într-un caz particular asupra unei asignări de probabilitate. Din contră, partea
cea mai grea nu este cea pur matematică, ci a aplicării teoriei. Problema anunțată
se compune din două complexe probleme: cea a sensului probabilității (Sinnproblem)
și cea a adecvării (Geltunasproblem). Ultima răspunde la întrebarea Cu ce drept
considerăm valabile axiomele calculului probabilităților la obiectele realului
? (pag. 338). În general, la celelalte sisteme axiomatice, problema adecvării
se rezolvă prin procedeul alegerii obiectului potrivit (geometria euclidiană,
mecanica, etc.). Dar axiomele nu se potrivesc niciodată realității; de aceea
problema adecvării celorlalte teorii formale la realitate se decide în cadrul
conceptului de probabilitate; așadar, dacă nu vrem să cădem într-un cerc vicios,
problema adecvării calculului probabilităților trebuie abordată diferit. La
o examinare mai atentă, problema adecvării se subîmparte în: (1) problema asignării
probabilității și (2) problema valabilității axiomelor. Dar, dacă probabilitatea
este o limită de frecvențe și axiomele I IV din Anexa 4 se verifică banal
la frecvențe, problema a doua nu se mai pune. Singura problemă cu adevărat grea
rămâne prima: cu ce drept considerăm că  ?
?
Pentru
a răspunde la întrebare, efectuează o scurtă incursiune în critica probabilităților
apriori, date prin considerente de simetrie. Ele se bazează pe principiul rațiunii
suficiente care constă în aceea că datorită simetriei zarului se înșală cine
crede că la o aruncare cinstită vreuna din fețe poate apărea mai ușor; la
o analiză mai atentă, acest mai ușor se dovedește a fi mai des, iar aceasta
este deja o incongruență logică deoarece nu se poate demonstra vreo legătură
logică între simetria zarului și frrecevnța apariției fețelor. În concluzie,
principiul rațiunii suficiente nu reușește să explice coerent asignarea probabilităților
chiar când uneori se potrivește. Însă egal probabilitatea aproximativă
se poate explica mai coerent prin metoda funcțiilor arbitrare a lui Poincaré,
care i se pare a fi o explicație mulțumitoare căci deducem egala probabilitate
din ipoteze mult mai slabe asupra repartiției inițiale. Oricum, am explicat
o probabilitate prin altă probabilitate; în ceea ce privește problema asignării
probabilității nu am progresat cu nimic în restul cazurilor.
Singura
speranță de lămurire a problemei asignării probabilității stă în probabilitatea
statistică, aposteriori. Dar interpretarea probabilității ca limită de frecvențe
împreună cu cerința ca șirurile să fie definite extensional colecții de date
statistice ne pune în situația absurdă că orice asertare probabilistică este
logic compatibilă cu orice segment inițial al șirului. Iar noi nu dispunem decât
de segmente inițiale ale lui care sunt neglijabile în raport cu restul. O propoziție
de genul 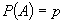 afirmă
existența unei infinități de termeni ai șirului cu proprietatea A; însă aceasta
este o afirmație complet nedecidabilă empiric.
afirmă
existența unei infinități de termeni ai șirului cu proprietatea A; însă aceasta
este o afirmație complet nedecidabilă empiric.
În concluzie
dorim tratarea șirurilor probabiliste date intensional prin calculul probabilităților,
iar a celor date extensiv prin calculul aplicat probabilităților. În primul
caz afirmațiile sunt decidabile matematic, în al doilea nedecidabile... Interpretarea
frecvențialistă a probabilității duce la afirmații complet nedecidabile. Asertarea
limitei are un caracter de profeție și anume al unei profeții complet
nedecidabile. Aici este sâmburele tuturor greutăților epistemologice ale conceptului
de probabilitate. Atât problema adecvării cât și a sensului duc la întrebări
care par de neînvins.
Ar fi
prea comod ca în fața acestei situații, aparent fără ieșire să dăm înapoi considerând
întreaga problemă ca fiind lipsită de sens, consideră în continuare autorul.
Nu este fără sens să pretinzi că un șir are limită. Numai că este vid logic
(leer). Ceea ce se pune în discuție este caracterul intensiv (Inhaltlichkeit)
al interpretării frecvențialiste. Se pare că interpretarea frecvențială (Häufigkeitsdeutung)
are același păcat pe care l+am reproșat interpretării probabilității ca referindu-se
la un caz unic (Einzelfallsdeutung): nu o putem corela cu vreo stare de fapt
(pag. 354). Din această situație absurdă am putea ieși prin două metode:
A. Să
căutăm altă interpretare frecvențială a probabilității, nu neapărat de limită
(se ștei că intepretarea Kolmogorov Cramér este tot frecvențială, dar probabilitatea
este gândită ca un punct în jurul căruia oscilează frecvențele parțiale, în
serii de experimente suficient de mari). Pentru Reichenbach, însă, și această
intepretare postulează existența unei limite; via teorema Bernoulli se ajunge
iarăși la teorema limitei, și din nou este o intepretare indecidabilă. Înseamnă
că necesitatea axiomei limitei este de neînlăturat din moment ce ne-am hotărât
la o intepretare frecvențială. Trebuie să încercăm rezlovarea dificultăților
logice legate de intepretarea probabilității ca limită altfel (pag. 358).
B. Totuși,
în realitate, problema nu este deloc nedecidabilă; în practică nu ne dăm înapoi
de la a pune asertări de frecvență sub formă de limită... și deosebim foarte
bine între o propoziție și negarea ei. Dacă, de exemplu, la aruncarea unui zar
de 6000 de ori apar 990 de 6 accept că 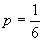 iar dacă
au apărut numai 10, resping fără șovăială aceeași ipoteză. Și totuși, am văzut
că din punct de vedere logic, orice asertare de limită este vidă de conținut
pentru șiruri date extensiv, fiind compatibilă cu orice segment inițial. Înseamnă
că logica noastră bivalentă este de vină și trebuie dată la o parte dacă nu
vrem să renunțăm la teoria probabilităților, transformând-o, prin renunțarea
la asertarea limitei într-o arhivă, o colecție stupidă de date fără valoare
predictivă. Și adevărul este că nici noi nu gândim după logica bivalentă, care
nu e decât o idealizare care se potrivește în mai multe cazuri tocmai pentru
că se neglijează latura probabilistă a cunoașterii (pag. 359). Credem că nu
se va putea lămuri niciodată problema adecvării teoriei probabilităților în
cadrul logicii clasice, căci în realitate, judecarea unei aserțiuni probabiliste
este ea însăți un demers probabilist (pag. 359). Trecerea la logica probabilistă,
este clar că Reichenbach nu o face ca un scop în sine: nu poate rezolva altfel
problema. Ea are caracterul saltului de la geometria euclidiană la cea riemanniană.
Logica clasică nu este decât un caz degenerat al logicii adevărate, reale a
omului, Dominarea psihologică a ei ține de aceleași resorturi ca și dominarea
psihologică a geometriei euclidiene (pag. 360).
iar dacă
au apărut numai 10, resping fără șovăială aceeași ipoteză. Și totuși, am văzut
că din punct de vedere logic, orice asertare de limită este vidă de conținut
pentru șiruri date extensiv, fiind compatibilă cu orice segment inițial. Înseamnă
că logica noastră bivalentă este de vină și trebuie dată la o parte dacă nu
vrem să renunțăm la teoria probabilităților, transformând-o, prin renunțarea
la asertarea limitei într-o arhivă, o colecție stupidă de date fără valoare
predictivă. Și adevărul este că nici noi nu gândim după logica bivalentă, care
nu e decât o idealizare care se potrivește în mai multe cazuri tocmai pentru
că se neglijează latura probabilistă a cunoașterii (pag. 359). Credem că nu
se va putea lămuri niciodată problema adecvării teoriei probabilităților în
cadrul logicii clasice, căci în realitate, judecarea unei aserțiuni probabiliste
este ea însăți un demers probabilist (pag. 359). Trecerea la logica probabilistă,
este clar că Reichenbach nu o face ca un scop în sine: nu poate rezolva altfel
problema. Ea are caracterul saltului de la geometria euclidiană la cea riemanniană.
Logica clasică nu este decât un caz degenerat al logicii adevărate, reale a
omului, Dominarea psihologică a ei ține de aceleași resorturi ca și dominarea
psihologică a geometriei euclidiene (pag. 360).
În sfârșit,
răspunsul la problema decidabilității este: probabilitatea nu este decidabilă
logic; ea este decidabilă inductiv; gândirea probabilistă este gândirea
inductivă (Der induktive Schluss ist ein Wahrscheinlichkeitsschluss pag. 10).
Când oamenii spun că anumite fapte justifică o ipoteză probabilistică și altele
nu, ei nu gândesc pe scara da nu, ci pe o scară continuă de valori.
Rezultă
că intrebarea: Cu ce drept asignăm probabilitatea p unui eveniment ?
are în spate întrebarea Cu ce drept folosim regula iducției ? Cu nici unul
dacă e să judecăm după logica normală; pentru că este singurul instrument
justificat de care dsipunem răspunde autorul, folosind logica probabilistă.
Regula inducției (dacă de n ori observi P, conchid că a
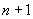 a oară
va apărea iarăși P) aplicată la frecvențe spune: dacă de n ori
observi frecvențele
a oară
va apărea iarăși P) aplicată la frecvențe spune: dacă de n ori
observi frecvențele  aproximativ
egale, inferă că tot așa va fi și a
aproximativ
egale, inferă că tot așa va fi și a  a oară.
Ea se bazează pe un pariu tacit al nostru: că lumea este previzibilă. În limbaj
probabilistic, că limita frecvenței există. Dacă este așa, regula inducției
ne va duce spre limită. Dacă nu, oricum ea este singura pe care o știm pentru
a prevedea. De aceea ea este justificată i se răspunde lui Hume. Un orb care
s-a rătăcit în munți, pipăie cu bastonul o cărare. El nu știe încotro duce această
cărare, nici dacă nu îl va arunca în prăpastie. Și totuși, în măsura în care
poate să o pipăie, el o va urma pas cu pas. Căci dacă pentru el există măcar
o posibilitate să ajungă undeva, aceasta este să-și pipăie în continuare cărarea.
În fața viitorului suntem ca acest orb; pipăim o cale (inducția n.n.) și știm:
dacă măcar un drum se poate găsi prin viitor, apoi acesta este de a pipăi în
continuare cu bastonul această cărare (pag. 420)
a oară.
Ea se bazează pe un pariu tacit al nostru: că lumea este previzibilă. În limbaj
probabilistic, că limita frecvenței există. Dacă este așa, regula inducției
ne va duce spre limită. Dacă nu, oricum ea este singura pe care o știm pentru
a prevedea. De aceea ea este justificată i se răspunde lui Hume. Un orb care
s-a rătăcit în munți, pipăie cu bastonul o cărare. El nu știe încotro duce această
cărare, nici dacă nu îl va arunca în prăpastie. Și totuși, în măsura în care
poate să o pipăie, el o va urma pas cu pas. Căci dacă pentru el există măcar
o posibilitate să ajungă undeva, aceasta este să-și pipăie în continuare cărarea.
În fața viitorului suntem ca acest orb; pipăim o cale (inducția n.n.) și știm:
dacă măcar un drum se poate găsi prin viitor, apoi acesta este de a pipăi în
continuare cu bastonul această cărare (pag. 420)
În fața
descoperirii incoerenței logice a inducției, Hume se resemnează. Din contră,
nici urmă de așa ceva la Reichenbach: Rezultatul nostru nu este resemnare:
căci am arătat că ar trebui să ne ghidăm după regula inducției chiar dacă nu
credem în ea... Să fie clar: noi nu știm dacă ordinea lumii nu se va
schimba, dacă soarele va mai răsări și mâine; poate mâine lumea va înceta pentru
noi, deoarece vom fi închis ochii pentru totdeauna. Dar aceasta nu schimbă rațiunile
care ne determină acțiunile. Ne bazăm acțiunile pe ideea că lumea este previzibilă;
dacă nu este așa, ei bine, am acționat în zadar. (pag. 420)
Tot în
cadrul curentului frecvențialist l-aș încadra și pe K. Popper (1902 -
??). Cel puțin așa se prezintă în lucrarea sa Logica cercetării, pe care o
voi comenta. Mai târziu (1959), a ajuns la concluzia că tratarea probabilității
pe baza teoriei măsurii trebuie preferată interpretării frecvențiale atât din
motive matematice, cât și filosofice interpretarea probabilității ca măsură
a tendinței de realizare([47], pag.243). În schimb, în [47], un întreg capitol, plus anexe adăugate
în decursul anilor, sunt deidcate unei încercări de fundare frecvențialistă
a probabilității. Spre deosebire de Reichenbach, care vrea să renunțe la Regellosigkeit
păstrând axioma limitei, Popper speră să reușească o construcție în care, slăbind
axioma hazardului să renunțe la axioma limitei, decretată vinovata principală
în dificultățile de interpretare ale teoriei.
Întâi
o observație matematică. Șirurile absolut libere ale lui Popper, discutate
în §1.2, au într-adevăr proprietatea că, empiric, ele sunt mai aleatoare decât
ale lui von Mises, în sensul că mecanismul aleator începe să lucreze chiar de
la început. Dar tratarea matematică a probalemei nu este riguroasă: în puctul
cheie ([47],§64) unde era vorba să renunțe la axioma limitei, Popper devine
brusc neinteligibil, cu toate comentariile și anexele adăugate ulterior. Problema
ar fi fost să definească noțiunea de șir absolut liber infint (de 0 și 1 măcar)
și apoi să demonstreze că un asemenea șir absolut liber are proprietatea că frecvențele parțiale converg spre
o anumită limită. Tot ceea ce reușește să facă este să construiască exemple
particulare de șiruri absolut libere cât mai scurte posibil (în sensul că segmentele
inițiale de lungime 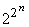 sunt
n libere) a căror
frecvență parțială tinde la
sunt
n libere) a căror
frecvență parțială tinde la 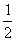 . Nu văd
cum se trece apoi la un p oarecare. În plus folosește noțiunea de frecvență
medie absolut liberă (pag. 196) pe care nu o definește, deși este esențială
pentru construcția pretinsă.
. Nu văd
cum se trece apoi la un p oarecare. În plus folosește noțiunea de frecvență
medie absolut liberă (pag. 196) pe care nu o definește, deși este esențială
pentru construcția pretinsă.
O explicație
simplă a preocupărilor îndelungate ale lui Popper pentru conceptul de probabilitate
este aceea că este greu de împăcat cu ideile sale deductivist falsificaționiste
privind teoriile științifice. Cartea [47] este o replică destul de polemică la adresa inducționismului probabilist al
lui Reichenbach, comentat mai sus. Sarcina pe care și-o asumă este
(1) Crearea
unei noi baze pentru calculul probabilităților pe linia deschisă de von Mises:
o teorie frecvențialstă eliberată de axioma limitei, și
(2) Clarificarea
relației existente între o aserțiune probabilistică și experiență: problema
decidabilității.
Ne vor
interesa în primul rând supozițiile ontologice explicite sau tacit admise pe
care la face referitor la probabilitatea fizică, și nu a ipotezelor sau a teoriilor.
De altfel, sunt de acord mai degrabă cu el decât cu Reichenbach că nu se poate
atașa vreo probabilitate obiectivă unei teorii științiifice. O asertare de tipul
P(teoria lui Schrödinger este adevărată | experiența acumulată) = p mi se pare un nonsens, sau cel mult un joc
inutil cu simbolurile probabilistice. Pare clar că ceea ce intenționează este
consolidarea unei probabilități obiective, așa cum este necesară în fizică,
unde din păcate persistă o situație inacceptabilă: fitâzica operează cu probabilități
fără a fi în stare să formuleze în mod consistent ce se înțelege prin ele (pag.
165). Interpretarea care părea să realizeze acest deziderat îi părea, atunci,
cea frecvențialistă: ...voi încerca să reconstruiesc teoria probabilității
ca o teorie frecvențialistă (modificată). Mă declar prin aceasta adeptul unei
interpretări obiective, în primul rând deoarece cred că numai o asemenea teorie
obiectivă poate explica aplicarea calculului probabilităților în științele
empirice. Teoria subiectiv, care de altfel are de învins mai puține dificultăți
de ordin logic decât cea obiectivă, poate, este adevărat, să dea un răspuns
logic consistent problemei decidabilității enunțurilor probabiliste, dar, cum
acest răspuns ar trebui să conceapă aceste anunțuri ca fiind tautologice, deci
neempirice, nu ne putem declara mulțumiți cu răspunsul oferit de ea, dacă ne
gândim la aplicațiile fizice ale teoriei probabilităților (pag. 168). Problema
fundamentală a teoriei hazardului este cum un enunț despre ceea ce nu știm,
interpretat ca enunț frecvențial poate fi testat și coroborat empiric. (pag.
169).
Spre deosebire
de ceilalți frecvențialiști și critici ai teoriei lui von Mises care au combătut
mai ales axioma hazardului, considerând-o o monstruozitate matematică (P.
Servien) și cerând renunțarea la ea (Kamke, Dörge, Reichenbach) Popper resimte
mai mult necesitatea epistemologică a eliminării axiomei limitei... care nu
este mai puțin problematică decât cea a hazardului (pag.171) deoarece limita
unui șir nu este altceva decât o proprietate caracteristică a legii sau regulii
matematice prin care este definit șirul (pag. 171) și ea are forma unui enunț
universal nefalsificabil... care nu poate avea nici un conținut extensional,
ci numai intensional. (pag. 203).
Problema
cea mai dificilă este cea epistemologică a aplicării teoriei probabilităților.
Conform punctului său de vedere, o teorie este științifică, și nu metafizică,
numai în măsura în care poate produce enunțuri falsificabile, adică dacă se
poate imagina un test la care, dacă ar eșua, să fie respinsă. Or, enunțurile
de probabilitate nu sunt falsificabile, nefalsificabilitatea logică a enunțurilor
de probabilitate este în afară de orice îndoială; aplicabilitatea lor în științele
empirice pare să zguduie din temelii întreaga mea concepție epistemologică
(pag. 199). Să fie atunci toată teoria probabilităților o întreprindere metafizică
?
Autorul
încearcă să soluționeze problema tocmai prin aplicarea consecventă a acestei
concepții (falsificaționiste) (pag. 199). Primul pas constă în analiza formei
logice a enunțurilor de probabilitate. Dacă este să găsim un răspuns, apoi
acesta trebuie să fie în cadrul logicii obișnuite; Popper nu resimte nevoia
unei logici probabiliste pentru că este pe de-a-ntregul posibil ca relațiile
probabiliste să fie supuse unei analize complete efecutată în cadrul relațiilor
clasice de deductibilitate și contradicție. Analiza logică arată că orice enunț
de probabilitate este neempiric, iar noi avem pretenția să îl falsificăm empiric.
Să presupunem că în urma a 100 de aruncări cu banul apare numai stema. Deoarece
avem bun simț, vom renunța la ipoteza că  . De ce
? Nu putem observa decât o serie finită, și în cadrul ei probabilitatea unei
succesiuni de 100 de steme, deși foarte mică, este totuși pozitivă. Speranța
că raritatea calculată a unui asemenea fenomen constituie un mijloc de falsificare
a estimării probabilistice se dovedește a fi iluzorie, întrucât orice apariție
frecventă a unor segmente lungi foarte divergente poate fi oricând considerată
ca nefiind altceva decât un segment mai lung și mai divergent pentru care sunt
valabile aceleași considerații: nu există nici un șir de evenimente determinat
extensional... care ar putea falsifica un enunț de probabilitate (pag. 199).
De aceea, ipotezele probabiliste ar trebui considerate ca neinformative din
punct de vedere empiric !
. De ce
? Nu putem observa decât o serie finită, și în cadrul ei probabilitatea unei
succesiuni de 100 de steme, deși foarte mică, este totuși pozitivă. Speranța
că raritatea calculată a unui asemenea fenomen constituie un mijloc de falsificare
a estimării probabilistice se dovedește a fi iluzorie, întrucât orice apariție
frecventă a unor segmente lungi foarte divergente poate fi oricând considerată
ca nefiind altceva decât un segment mai lung și mai divergent pentru care sunt
valabile aceleași considerații: nu există nici un șir de evenimente determinat
extensional... care ar putea falsifica un enunț de probabilitate (pag. 199).
De aceea, ipotezele probabiliste ar trebui considerate ca neinformative din
punct de vedere empiric !
Dar împotriva
unei asemenea concluzii vorbește marele succes predictiv realizat în fizică
prin folosirea unor estimări ipotetice de probabilități (cinetica moleculară,
termodinamica statistică). Statistica se bazează pe falsificabilitatea practică
care constă în a considera că ipotezele prea improbabile sunt excluse.
Răspunsul
lui Popper, cu care rezlovă problema decidabilității, este că teoriile probabilistice,
atunci când sunt aplicate fără restricții nu pot fi caracterizate ca științifice:
trebuie să excludem utilizarea lor în metafizică, dacă vrem ca ele să fie de
vreun folos în practica științei empirice (pag. 205). Ca exemplu de cum nu
trebuie aplicate teoriile probabiliste, el dă, de exemplu cazul speculațiilor
asupra entropiei de genul este aproape cert că lumea se va dezagrega prin ea
însăți în mod accidental, dacă așteptăm suficient de mult deoarece teoria
probabilităților ne învață că un eveniment de probabilitate pozitivă se va produce
o dată și o dată. Într-adevăr, un asemenea mod de a pune problema denotă o
ontologizare naivă a probabilității și sunt de acord că nu are ce căuta în știință.
Dar cum
trebuie atunci aplicate probabilitățile în practica științifică ? Popper caută
(și consideră că găsește) răspunsul sperat în fizică. Problema decidabilității
creează dificultăți numai epistemologului, dar nu și fizicianului (pag. 205)
iar fizica a obținut succese spectaculoase. Așadar trebuie studiat statutul
probabilității în fizică. Problema fundamentării satisfăcătoare a probabilității
în fizică a fost și mai este încă (vezi [14]) dezbătută de multe generații de fizicieni,
adesea paralel și independent de matematicieni. Pentru Ehrenfest, arată Popper
(pag.205), aplicarea probabilității în fizică este o problemă conceptuală și
epistemologică. Fizicianul lucrează cu ea ca și cu o frecvență ideală, postulând
că adevăratele frecvențe nu se vor abate prea mult de la ea. Fizicianul adoptă
regula metodologică dictată de bunul simț de a nu explica niciodată efecte
fizice, regularități reproductibile prin acumulări de accidente (pag. 206).
Am ajuns
la conceptul cheie cu care Popper propune ieșirea din hățișul problemelor aparent
fără răspuns legate de decidabilitatea enunțurilor probabilistice: acela de
efect reproductibil. Se poate imagina, arată el, că într-un recipient cubic
de 1mc de aer, toate moleculele se vor deplasa spontan în sus și nu vor atinge
marginea de jos a recipientului. Probabilitatea unui asemenea eveniment în cadrul
modelului Boltzmann ar fi de ordinul lui  -
un număr atât de mic, încât este imposibil de imaginat. Dar un asemenea fenomen
nu va putea apărea niciodată ca un efect fizic, deoarece datorită extremei
sal improbabilități el nu ar putea fi reprodductibil după voie. Chiar dacă un
fizician ar putea observa un asemenea proces, el ar fi incapabil să îl reproducă
și de aceea nu ar putea decide ce s-a întâmplat în realitate și dacă nu cumva
a făcut o eroare de observație. Dacă însă, abaterile de la un macroefect dedus
prin ipoteze probabiliste sunt reproductibile, presupunem că estimarea probabilistă
a fost falsificată.
-
un număr atât de mic, încât este imposibil de imaginat. Dar un asemenea fenomen
nu va putea apărea niciodată ca un efect fizic, deoarece datorită extremei
sal improbabilități el nu ar putea fi reprodductibil după voie. Chiar dacă un
fizician ar putea observa un asemenea proces, el ar fi incapabil să îl reproducă
și de aceea nu ar putea decide ce s-a întâmplat în realitate și dacă nu cumva
a făcut o eroare de observație. Dacă însă, abaterile de la un macroefect dedus
prin ipoteze probabiliste sunt reproductibile, presupunem că estimarea probabilistă
a fost falsificată.
Se propune,
în definitiv, următorul răspuns paradoxal: (pag. 209) Întrebare: cum pot ipotezele
probabilistice care nu sunt falsificabile juca rolul unor legi naturale în știința
empirică ? Iată răspunsul: În măsura în care nu sunt falsificabile, enunțurile
probabilistice sunt metafizice și lipsite de semnificație empirică; în măsura
în care apar ca enunțuri empirice, ele sunt utilizate ca enunțuri falsificabile.
Întrebare: Cum pot enunțurile probabilistice care nu sunt falsificabile să fie
utilizate ca enunțuri falsificabile ?... Printr-o regulă metodologică care...
interzice producerea, susceptibilă de a fi prevăzută și reprodusă unor abateri
sistematice, cum ar fi abaterile într-o direcție anumită sau producerea unor
segmente care sunt atipice într-un fel anumit. Ea cere nu o simplă corespondență
aproximativă, ci cea mai bună concordanță pentru ceea ce poate fi reprodus și
testat pentru toate efectele..
Să fiu
sincer, nu știu care statistician ar fi mulțumit cu o asemenea ieșire din impas.
Nu ni s-a spus nimic despre judecata pe care o face cineva în asignarea unei
probabilități, cu ce drept consideră că  . Ca să
infirm această afirmație ar trebui să reproduc după voie o frecvență diferită
cu mult de
. Ca să
infirm această afirmație ar trebui să reproduc după voie o frecvență diferită
cu mult de 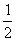 ? Nu
este o pretenție cam prea severă ? Dacă cineva aruncă un zar de 600 de ori și
nu apare nici un 6, el renunță fără nici o ezitare la ipoteza
? Nu
este o pretenție cam prea severă ? Dacă cineva aruncă un zar de 600 de ori și
nu apare nici un 6, el renunță fără nici o ezitare la ipoteza 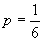 , fără
a considera necesar să mai reproducă efectul, fiindcă este convins că ceea ce
este prea puțin probabil nu se întâmplă, deși acest lucru i se pare iluyoriu
lui Popper. Și, în definitiv, de unde știu că un efect este reproductibil sau
nu ? Nu cumva se intră într-un cerc vicios respingând criteriul de falsificare
al improbabilității și înlocuindu-l cu cel de efect reproductibil ?
, fără
a considera necesar să mai reproducă efectul, fiindcă este convins că ceea ce
este prea puțin probabil nu se întâmplă, deși acest lucru i se pare iluyoriu
lui Popper. Și, în definitiv, de unde știu că un efect este reproductibil sau
nu ? Nu cumva se intră într-un cerc vicios respingând criteriul de falsificare
al improbabilității și înlocuindu-l cu cel de efect reproductibil ?
Von Mises
și Popper au meritul, după părerea mea, de a fi pus în evidență faptul că legile
statistice nu pot fi niciodată reduse la cele deterministe. Nici cea mai neînsemnată
teoremă a teoriei cinetice a gazelor nu derivă din fizica clasică fără ajutorul
unor ipoteze de ordin statistic spune von Mises (citat din [47], pag. 212). Explicația dată de Popper este că în orice
derivare de legi statistice (= enunțuri de frecvență)
intervin ipoteze de natură statistică asupra condițiilor inițiale. Pe scurt,
concluziile probabiliste cer premise probabiliste.
În general,
sunt de acord cu ireductibilitatea probabilității la altceva. Anumite dubii
le voi discuta în Anexa 3.
Rezolvarea
de către Popper a problemei cazului unic concordă cu cea a lui Reichenbach.
Când unui caz unic i se atașează o probabilitate, se are în vedere întotdeauna
o clasă de referință, măcar tacit. Natural că inserarea cazului în clase de
referință diferite produce asignarea de probabilități diferite. Așa și apar
multe paradoxuri probabibliste neinteresante. Probabilitatea unui caz unic
este denumită de Popper formalistă (§71) și este văzută ca o punte de legătură
cu teoria subiectivistă a lui Keynes: Putem accepta să interpretăm (urmându-l
pe Keynes) o probabilitate formalistă ca grad al încrederii raționale, cu
condiția însă ca încrederea rațională să fie determinată de un enunț frecvențial
obiectiv, acesta din urmă constituind atunci informația care determină gradul
de încredere. Cu alte cuvinte, exceptând faptul că el aparține unei clase de
referință în cadrul căreia o anumită estimare probabilistă este coroborată;
această informație
ne va permite să exprimăm tot ce știm despre el prin intermediul
unui enunț probabilistic formalist care apare ca o predicție nedeterminată despre
evenimentul singular în cauză.
Ceea ce
respinge și pe drept cuvânt, consider este pretenția ca enunțurile de probabilitate
formaliste să fie interpretate nemijlocit obiectiv (  la o
aruncare cu zarul ar însemna că rezultatul următoarei aruncări cu zarul ar fi
în mod obiectiv nedefinit și nedeterminat).
la o
aruncare cu zarul ar însemna că rezultatul următoarei aruncări cu zarul ar fi
în mod obiectiv nedefinit și nedeterminat).
De asemenea,
Popper are o interpretare interesantă, statistică, a relațiilor de incertitudine
ale lui Heisenberg pe care le consideră relații statistice de împrăștiere. Nu
este de competența mea să fac vreo apreciere asupra punctului său de vedere.
Remarc numai că punctul său de vedere asupra interpretării conceptului de probabilitate
s-a modificat: în lucrările mai noi (1959) optează pentru o interpretare propensionalistă
moderată, adică corelată cu noțiunea de frecvență.
Deși poate
că nu este întru totul justificat, m-am decis să discut lucrarea Voraussage,
Wahrscheinlichkeit, Object de M. Drieschner (1979) (Predicție, probabilitate,
obiect) la capitolul despre frecvențialism. Cartea nu este de matematică, ci
de fundamentele fizicii. Pe autor îl interesează mai mult noțiunea de probabilitate
de care are nevoie fizicianul. Motivul pentru care îl includ la frecvențialiști
este definiția pe care o dă probabilității (§IV, 4): Probabilitatea este frecvența
relativă prevăzută. Așadar, probabilitatea se referă la colecții de evenimente,
finite dar oricât de mari, și ea este o conjectură privind componența
așteptată a setului de date experimentale. Este o definiție mergând pe ideea
lui Ehrenfest comentată mai sus. Sigur că matematicianul ar putea obiecta că
la un set de 10 probe nu are sens să prevezi o frecvență relativă de 0,13, adică
nu este prea riguros să legi frecvența prevăzută de numărul probelor, însă aceasta
se poate aranja fără complicații prea mari. Important este că definiția este
practică pentru experimentator: De la o definiție bună trebuie să te aștepți
să regăsești sensul uzual al termenului și să fie practică pentru tema propusă
(§4.4). De altfel abundența propunerilor teoriei probabilităților aproape că
te înspăimântă. Adesea, oameni diferiți propun teorii care răspund la întrebări
diferite( §4.4). Întrebările care așteaptă răspuns, și la care autorul crede
că a găsit un răspuns parțial sunt:
1. Ce
este probabilitatea ?
2. Cum
se asignează o probabilitate unui eveniment ?
3. Cum
pot verifica empiric enunțuri probabilistice ?
4. Cum
pot să știu dacă un șir de evenimente sunt independente și au aceeași probabilitate
?
Definirea
probabilității ca o frecvență relativă prevăzută este o definiție subliniază
Drieschner deoarece în capitolele anterioare ale cărții autorul a discutat
conceptul de predicție (Voraussage). Referentul predicției nu este un subiect
individual, ci unul epistemologic: prin această precizare termenul capătă și
o încărcătură obiectivă. Printre predicții există și predicțiile de frecvență;
ele sunt un tip de legi ale naturii sui generis, numite statistice. Probabilitatea
cu care avem de a face în fizică este întotdeauna o frecvență prezisă: O frecvență
relativă prevăzută este cea mai generală predicție care se poate proba empiric
(§4.6). Legile naturii nu sunt numai de tipul Da sau Nu, ci și de tipul
Uneori da, alteori nu. În ultimele intră probabilitatea ca ceva care se aplică
la predicții în viitor, o cuantificare a posibilității(§4.4). Conexiunea posibilității
cu predicția se face prin frecvanță: În aplicarea practică a probabilității
în științele naturii interpretarea frecvențială este inevitabilă (§4.4).
A defini
probabilitatea ca frecvență relativă prevăzută, nu spune însă prea mult dacă
nu se lămurește cum apar predicțiile de frecvență, cum pot fi ele probate
empiric și când sunt ele posibile.
Predicțiile de frecvență apar fie
empiric, în urma unui șir de experimente efectuta în condiții practic identice,
postulând că frecvența viitoare nu se va deosebi prea mult de cea găsită (asignarea
statistică), fie din considerente de simetrie, așa cum se face în teoria cinetică
a gazelor (asignarea apriori).
Ambele
metode nu sunt irefutabile logic, însă este o stare de fapt că se potrivesc
mulțumitor. Frecvența relativă coincide numai aproximativ cu cea prezisă. Dar
nu prin acest lucru se deosebește probabilitatea de celelalte cantități măsurabile,
căci orice măsurătoare se abate de la adevărata valoare prin ceva. Caracterul
fundamental al măsurării probabilității este că eroarea scade numai probabil
odată cu creșterea numărului probelor. La asignarea statistică a probabilităților
problema nu mai este predicția frecvenței relative pentru viitoare măsurări,
ci fixarea unei frecvențe precizate din datele disponibile. Problema unei predicții
corecte nu ar avea nici un sens dacă nu ar avea în vedere o lege a naturii din
acre urmează predicția. Frecvența relativă precizată poate servi la aceea că
din mai multe predicții logic posibile să o alegem pe cea care se potrivește
în realitate cel mai bine(§4.7a). În asignarea statistică, nu se mai caută
probabilitatea unui eveniment în condițiile unei ipoteze (ipoteza este deja
probabilistă, că 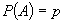 n.n.)
ci invers, probabilitatea unei ipoteze dacă evenimentul fixat se întâmplă
(§4.7a). Lucrurile se complică deoarece probabilitatea unei ipoteze nu mai are
interpretare frecvențială: ea este într-un grad și mai mare ipotetică, fiind
derivată prin regula lui Bayes sau prin metoda verosimilității maxime (regula
likelihoodului, care în cazul cel mai simplu, a două ipoteze h și h spune: dacă
n.n.)
ci invers, probabilitatea unei ipoteze dacă evenimentul fixat se întâmplă
(§4.7a). Lucrurile se complică deoarece probabilitatea unei ipoteze nu mai are
interpretare frecvențială: ea este într-un grad și mai mare ipotetică, fiind
derivată prin regula lui Bayes sau prin metoda verosimilității maxime (regula
likelihoodului, care în cazul cel mai simplu, a două ipoteze h și h spune: dacă  , acceptă
pe h). Prima regulă cere cunoașterea probabilităților apriori ale ipotezelor,
lucru foarte convențional și arbitrar; în schimb metoda a doua duce la rezultate
absurde, mai ales la eșantioane mici: de exemplu, dacă la o serie de trei aruncări
cu banul au apărut numai steme și dacă am aplica aniv regula verosimilității
am decreta că P(stemă) = 1 ! Pe lângă acaestă obiecție, mai
există un contraexemplu celebru (jocul cu bile al lui Ehrenfest) care arată
că metoda verosimilității ne duce la concluzii false. De aceea, Drieschner propune
următoarea metodologie de asignare a frecvenței relative prevăzute: Un eveniment
întotdeauna repetabil face în timp acea ipoteză mai probabilă care acordă
acestui eveniment, în ipotezele posibile, probabilitatea maximă (§4.7a). Cu
alte cuvinte, trebuie urmărit șirul
, acceptă
pe h). Prima regulă cere cunoașterea probabilităților apriori ale ipotezelor,
lucru foarte convențional și arbitrar; în schimb metoda a doua duce la rezultate
absurde, mai ales la eșantioane mici: de exemplu, dacă la o serie de trei aruncări
cu banul au apărut numai steme și dacă am aplica aniv regula verosimilității
am decreta că P(stemă) = 1 ! Pe lângă acaestă obiecție, mai
există un contraexemplu celebru (jocul cu bile al lui Ehrenfest) care arată
că metoda verosimilității ne duce la concluzii false. De aceea, Drieschner propune
următoarea metodologie de asignare a frecvenței relative prevăzute: Un eveniment
întotdeauna repetabil face în timp acea ipoteză mai probabilă care acordă
acestui eveniment, în ipotezele posibile, probabilitatea maximă (§4.7a). Cu
alte cuvinte, trebuie urmărit șirul  ;
;
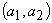 ;
;
 ;...;
;...;
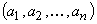 și căutată
acea probabilitate p pentru care această evoluție are probabilitatea
maximă. Este vorba de o modificare a metodei verosimilității, posibil (principial)
de aplicat cu ajutorul calculatoarelor.
și căutată
acea probabilitate p pentru care această evoluție are probabilitatea
maximă. Este vorba de o modificare a metodei verosimilității, posibil (principial)
de aplicat cu ajutorul calculatoarelor.
A doua
metodă de asignare este cea apriori, dată de considerente de simetrie. Ea poate
servi de substitut pentru probabilitățile apriori care lipsesc la aplicarea
teoremei Bayes. Nu trebuie ontologizată asignarea probabilității pe baza aplicării
numai a principiului rațiunii suficiente, deoarece s-a arătat (von Mises,
Popper, Reichenbach) că aceasta este greșit. Aproximațiile date pe baza lui
pot fi folosite însă mai departe în aplicarea teoremei Bayes, căci ele nu se
pot abate prea mult de adevăr: Totuși, în acest raționament (al rațiunii suficiente,
n.n.) este și ceva adevărat. Presupunerea că toate fețele unui zar sunt echiprobabile
este adevărată (? Cred că autorul a vrut să spună nu este prea neadecvată
n.n.) dacă fețele nu se deosebesc unele de altele prin nimic. Faptul
că ele sunt identice nu traduce o lipsă de cunoaștere, ci o stare de fapt.
Această ultimă restricție este importantă. La un zar real echivalența ar fi
mai mult sau mai puțin adevărată. Predicția se face pe baza ei și se va potrivi
în măsura în care este îndeplinită (§4.7b). (Nu trebuie luat prea în serios
ultimul rând, căci el pare să contrazică punctele de vedere exprimate anterior
ale autorului: ad literam, ar fi o revenire la punctul de vedere al lui Cournot
că probabilitatea 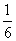 este
o proprietate fizică a zarului, ceea ce, evident nu se poate susține).
Este vorba numai despre o primă aproximație, necesară în abordări ulterioare:
În fizică, probabilitățile se vor aplica mai ales în aceste cazuri, adesea
cu ajutorul unor calcule din teoria grupurilor (§4.7b).
este
o proprietate fizică a zarului, ceea ce, evident nu se poate susține).
Este vorba numai despre o primă aproximație, necesară în abordări ulterioare:
În fizică, probabilitățile se vor aplica mai ales în aceste cazuri, adesea
cu ajutorul unor calcule din teoria grupurilor (§4.7b).
Pentru
a putea folosi teoria propusă, Drieschner are nevoie și de ipoteze de ordin
doi, asupra frecvenței frecvențelor. Ele rezultă din ipoteze de independență,
care cred că nu poate fi decât aproximativă, din moment ce se lucrează cu frecvențe,
fie ele și prevăzute (Evenimentele A și B, provenite de la două alternative
compatibile adică putându-se observa împreună, ceea ce nu este superfluu,
căci în mecanica cuantică nu orice măsurători sunt compatibile, ci numai dacă
aparțin aceleiași algebre Boole sunt independente dacă 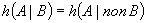 ), unde
h este frecvența relativă prevăzută; lucrul nu este posibil, stricto
sensu, decât dacă
), unde
h este frecvența relativă prevăzută; lucrul nu este posibil, stricto
sensu, decât dacă 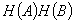 este
diviyibil prin N unde H înseamnă frecvența absolută, iar N
numărul probelor. Așa că definiția trebuie interpretată nuami aproximativ, eventual
folosindu-se funcția parte întreagă).
este
diviyibil prin N unde H înseamnă frecvența absolută, iar N
numărul probelor. Așa că definiția trebuie interpretată nuami aproximativ, eventual
folosindu-se funcția parte întreagă).
p.91 2 sept. 2001
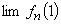 există,
unde
există,
unde 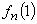 este
frecvența relativă a apariției unui 1 în primii n termeni ai șirului
rezultatelor experimentului. Dar nu toate șirurile de acest fel sunt bune. Nimeni
nu va pretinde că dacă la o aruncare cu banul apare șirul 00110011001100110011....
aruncarea a fost cinstită, deși limita frecvenței relative (sau limita Venn,
cum se mai numește) există și este egală cu
este
frecvența relativă a apariției unui 1 în primii n termeni ai șirului
rezultatelor experimentului. Dar nu toate șirurile de acest fel sunt bune. Nimeni
nu va pretinde că dacă la o aruncare cu banul apare șirul 00110011001100110011....
aruncarea a fost cinstită, deși limita frecvenței relative (sau limita Venn,
cum se mai numește) există și este egală cu 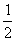 . Ar trebui
studiate numai șiruri aleatoare, care corespund unor aruncări reale. El nu
a putut rezolva problema definirii obiectelor de care avea nevoie.
. Ar trebui
studiate numai șiruri aleatoare, care corespund unor aruncări reale. El nu
a putut rezolva problema definirii obiectelor de care avea nevoie.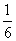 este
convins că va cădea 6 și
este
convins că va cădea 6 și 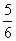 este
convins de contrariu, ci deoarece el știe că în serii lungi de aruncări 6
va apărea aproximativ într-o șesime din cazuri. Ce are a face acest lucru cu
un pariu la o singură aruncare contingentă ? Aceasta nu este decât traducerea
în practică a convingerii noastre asupra a ceea ce se petrece în serii mari
de aruncări răspunde Venn ([63],
§22). Pur și simplu este vorba
de o translatare a regulii care este justificată la serii lungi în cazul unui
singur pariu. Este un lucru relativ și depinzând de punctul de vedere al evenimentului
izolat sau al colectivului. Iată un alte exemplu ([63], §25): Știu că voi muri în una din cele 7 zile
ale săptămânii. Credința mea că voi muri într-o duminică este, deci,
este
convins de contrariu, ci deoarece el știe că în serii lungi de aruncări 6
va apărea aproximativ într-o șesime din cazuri. Ce are a face acest lucru cu
un pariu la o singură aruncare contingentă ? Aceasta nu este decât traducerea
în practică a convingerii noastre asupra a ceea ce se petrece în serii mari
de aruncări răspunde Venn ([63],
§22). Pur și simplu este vorba
de o translatare a regulii care este justificată la serii lungi în cazul unui
singur pariu. Este un lucru relativ și depinzând de punctul de vedere al evenimentului
izolat sau al colectivului. Iată un alte exemplu ([63], §25): Știu că voi muri în una din cele 7 zile
ale săptămânii. Credința mea că voi muri într-o duminică este, deci, 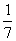 . Evenimentul
nu admite, în mod evident nici o repetare; totuși, nu credem cu toții la fel
?... Este adevărat că nu pot muri decât o dată, dar aparțin unei clase în care
moartea apare frecvent și opinia mea se formează după experiența acestei clase.
Dacă mi-aș asigura viața pentru 1000 lire, aș considera corect să cer 7000 dacă
societatea declară că nu va plăti decât decesele duminicale. Din puctul meu
de vedere, poate că nu ar fi prea echitabil, dar dacă toți ar fi asigurați confoem
acestui principiu, pentru societatea de asigurați conform acestui principiu,
pentru societatea de asigurări nu ar fi nici o diferență.
. Evenimentul
nu admite, în mod evident nici o repetare; totuși, nu credem cu toții la fel
?... Este adevărat că nu pot muri decât o dată, dar aparțin unei clase în care
moartea apare frecvent și opinia mea se formează după experiența acestei clase.
Dacă mi-aș asigura viața pentru 1000 lire, aș considera corect să cer 7000 dacă
societatea declară că nu va plăti decât decesele duminicale. Din puctul meu
de vedere, poate că nu ar fi prea echitabil, dar dacă toți ar fi asigurați confoem
acestui principiu, pentru societatea de asigurați conform acestui principiu,
pentru societatea de asigurări nu ar fi nici o diferență.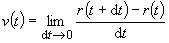 . Probabilitatea
se definește relativ la un colectiv prin limita frecvențelor
relative când n, numărul probelor, tinde la infinit. Nu are sens să ne
întrebăm dacă aceste limite există continuă el deoarece teoria pleacă exact
de la această supoziție. Fără viteză nu ar fi posibilă mecanica. Dacă viteza
există în realitate, nimeni nu poate ști sau verifica. Poate că mai degrabă
nu există și modelarea mișcării prin continuum nu este corectă. Dar, dacă noțiunea
de viteză nu ridică obiecții, de ce ar fi ele ridicate de noțiunea de probabilitate
ca limită a frecvențelor ?
. Probabilitatea
se definește relativ la un colectiv prin limita frecvențelor
relative când n, numărul probelor, tinde la infinit. Nu are sens să ne
întrebăm dacă aceste limite există continuă el deoarece teoria pleacă exact
de la această supoziție. Fără viteză nu ar fi posibilă mecanica. Dacă viteza
există în realitate, nimeni nu poate ști sau verifica. Poate că mai degrabă
nu există și modelarea mișcării prin continuum nu este corectă. Dar, dacă noțiunea
de viteză nu ridică obiecții, de ce ar fi ele ridicate de noțiunea de probabilitate
ca limită a frecvențelor ?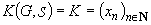 se numește
colectiv dacă: S este o familie de părți din S (corp de mulțimi);
G este o familie de place selections închisă la anumite operații grupale;
pentru orice mulțime
se numește
colectiv dacă: S este o familie de părți din S (corp de mulțimi);
G este o familie de place selections închisă la anumite operații grupale;
pentru orice mulțime  S
limita șirului
S
limita șirului  există
și se notează cu
există
și se notează cu 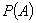 , unde
, unde
 este
frecvența termenilor din șirul K aparținând mulțimii A:
este
frecvența termenilor din șirul K aparținând mulțimii A:
 ; orice
place selection,
; orice
place selection, 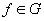 produce
un nou colectiv K cu proprietatea de convergență
anterioară. Wald [62] a demonstrat consistența noțiunii.
produce
un nou colectiv K cu proprietatea de convergență
anterioară. Wald [62] a demonstrat consistența noțiunii.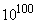 de 1 și
apoi 0 este permis în teoria sa ca un colectiv bine definit cu
de 1 și
apoi 0 este permis în teoria sa ca un colectiv bine definit cu  ,
,
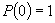 , față
de orice place selection; că în fizică am dori ca
, față
de orice place selection; că în fizică am dori ca 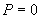 să însemne
imposibilitate fizică, iar dacă un fenomen apare de
să însemne
imposibilitate fizică, iar dacă un fenomen apare de  ori,
el este mai necesar fizic decât rotația pământului în jurul soarelui; nu vor
f, cu siguranță, mai mult de
ori,
el este mai necesar fizic decât rotația pământului în jurul soarelui; nu vor
f, cu siguranță, mai mult de  rotații
ale pământului în jurul axei sale până la dispariția sistemului solar. (Vârsta
universului este apreciată la cu mult mai puțin de
rotații
ale pământului în jurul axei sale până la dispariția sistemului solar. (Vârsta
universului este apreciată la cu mult mai puțin de 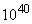 secunde
!)
secunde
!) - algebre
de evenimente: A este independent de B dacă
- algebre
de evenimente: A este independent de B dacă  ). Definiția
lui Kolmogorov a independenței pare mai degrabă o generalizare a unui concept
care are sens. Ea duce la inferențe care au foarte puțin de a face cu
semnificația general acceptată a termenului pe care se presupune că o reproduce.
([38], §1.10).
). Definiția
lui Kolmogorov a independenței pare mai degrabă o generalizare a unui concept
care are sens. Ea duce la inferențe care au foarte puțin de a face cu
semnificația general acceptată a termenului pe care se presupune că o reproduce.
([38], §1.10). nu poate
avea o semnificație reală. Enunțarea principiului stabilității frecvențelor
prin folosirea unei asemenea treceri la limită cere difinirea modurilor admise
de găsire a șirurilor infinite de experiențe care, iarăși nu poate fi decât
o ficțiune matematică. Toată această acumulare de noțiuni ar merita să fie supusă
unei analize serioase numai dacă s-ar obține ca rezultat construcția unei teorii
atât de specifice, încât fundamentarea ei riguroasă să se dovedească imposibilă
pe alte căi.
nu poate
avea o semnificație reală. Enunțarea principiului stabilității frecvențelor
prin folosirea unei asemenea treceri la limită cere difinirea modurilor admise
de găsire a șirurilor infinite de experiențe care, iarăși nu poate fi decât
o ficțiune matematică. Toată această acumulare de noțiuni ar merita să fie supusă
unei analize serioase numai dacă s-ar obține ca rezultat construcția unei teorii
atât de specifice, încât fundamentarea ei riguroasă să se dovedească imposibilă
pe alte căi. este
o implicație de un tip sui generis, o aserțiune privind apartenența unor obiecte
la o clasă. Toate probabilitățile sunt condiționate.
este
o implicație de un tip sui generis, o aserțiune privind apartenența unor obiecte
la o clasă. Toate probabilitățile sunt condiționate.  înseamnă
de fapt
înseamnă
de fapt 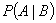 , unde
B se subînțelege.
, unde
B se subînțelege.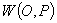 ; în al
doilea, a renunțat la ipoteza hazardului (regellosigkeit) ca fiind de nesusținut
logic.
; în al
doilea, a renunțat la ipoteza hazardului (regellosigkeit) ca fiind de nesusținut
logic. . Propoziția
. Propoziția
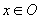
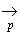
 se citește
se citește
 implică
probabilistoc de grad p că
implică
probabilistoc de grad p că  . În
știință, x se poate gândi ca premiză, cauză, condiție, context experimental,
iar y ca rezultat, efect. Notația prescurtată a propoziției de mai sus
este
. În
știință, x se poate gândi ca premiză, cauză, condiție, context experimental,
iar y ca rezultat, efect. Notația prescurtată a propoziției de mai sus
este 
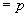 .
. -aditivă
și, în sfârșit pentru că nu este legată de o viziune ansamblistă ca axiomatizarea
lui Kolomogorov) dar care nu a fost adoptată de matematicieni (tocmai pentru
că era prea generală) ci numai de logicieni și filosofi. Sistemul său axiomatic
a apărut cu un an înaintea celui kolmogorovian (Ayiomatic der Wahrscheinlichkeitsrechnung,
Math. Zs., 34, 568 619, 1932). El este prezentat în Anexa 4.
-aditivă
și, în sfârșit pentru că nu este legată de o viziune ansamblistă ca axiomatizarea
lui Kolomogorov) dar care nu a fost adoptată de matematicieni (tocmai pentru
că era prea generală) ci numai de logicieni și filosofi. Sistemul său axiomatic
a apărut cu un an înaintea celui kolmogorovian (Ayiomatic der Wahrscheinlichkeitsrechnung,
Math. Zs., 34, 568 619, 1932). El este prezentat în Anexa 4.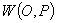
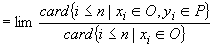 . Această
interepretare îl duce la un sistem axiomatic mai particular, o relaizare a celui
general în lumea șirurilor. Șirurile tip pentru care are sens să se vorbească
de probabilitate în interpretarea ei ca limită, le numește perechi normale de
șiruri, sau șiruri normale (cuvântul este luat de Borel, 1925, care îl folosea
în alt sens). Șirurile normale sunt o condiție mai slabă decât regellosigkeit-ul
lui von Mises. În principiu, lor nu li se cere decât să fie libere de influența
predecesorului și, dacă sunt împărțite în k subșiruri, numărând din k
în k, fiecare din subșirurile obținute să fie libere de influența predecesorilor. Definiția șirurilor
normale este și mai complicată decât axioma hazardului a lui Mises; în plus,
tratarea matematică este imposibilă pentru un matematician care are bunăvoința
să încerce să priceapă despre ce este vorba.
. Această
interepretare îl duce la un sistem axiomatic mai particular, o relaizare a celui
general în lumea șirurilor. Șirurile tip pentru care are sens să se vorbească
de probabilitate în interpretarea ei ca limită, le numește perechi normale de
șiruri, sau șiruri normale (cuvântul este luat de Borel, 1925, care îl folosea
în alt sens). Șirurile normale sunt o condiție mai slabă decât regellosigkeit-ul
lui von Mises. În principiu, lor nu li se cere decât să fie libere de influența
predecesorului și, dacă sunt împărțite în k subșiruri, numărând din k
în k, fiecare din subșirurile obținute să fie libere de influența predecesorilor. Definiția șirurilor
normale este și mai complicată decât axioma hazardului a lui Mises; în plus,
tratarea matematică este imposibilă pentru un matematician care are bunăvoința
să încerce să priceapă despre ce este vorba.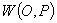
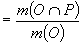 , unde
m este o măsură finit aditivă pe un corp de părți ale unei mulțimi generale
E. La kolmogorov se cere ca măsura să fie
, unde
m este o măsură finit aditivă pe un corp de părți ale unei mulțimi generale
E. La kolmogorov se cere ca măsura să fie
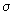 -aditivă,
deci o condiție mai tare.
-aditivă,
deci o condiție mai tare. ?
?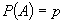 afirmă
existența unei infinități de termeni ai șirului cu proprietatea A; însă aceasta
este o afirmație complet nedecidabilă empiric.
afirmă
existența unei infinități de termeni ai șirului cu proprietatea A; însă aceasta
este o afirmație complet nedecidabilă empiric.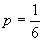 iar dacă
au apărut numai 10, resping fără șovăială aceeași ipoteză. Și totuși, am văzut
că din punct de vedere logic, orice asertare de limită este vidă de conținut
pentru șiruri date extensiv, fiind compatibilă cu orice segment inițial. Înseamnă
că logica noastră bivalentă este de vină și trebuie dată la o parte dacă nu
vrem să renunțăm la teoria probabilităților, transformând-o, prin renunțarea
la asertarea limitei într-o arhivă, o colecție stupidă de date fără valoare
predictivă. Și adevărul este că nici noi nu gândim după logica bivalentă, care
nu e decât o idealizare care se potrivește în mai multe cazuri tocmai pentru
că se neglijează latura probabilistă a cunoașterii (pag. 359). Credem că nu
se va putea lămuri niciodată problema adecvării teoriei probabilităților în
cadrul logicii clasice, căci în realitate, judecarea unei aserțiuni probabiliste
este ea însăți un demers probabilist (pag. 359). Trecerea la logica probabilistă,
este clar că Reichenbach nu o face ca un scop în sine: nu poate rezolva altfel
problema. Ea are caracterul saltului de la geometria euclidiană la cea riemanniană.
Logica clasică nu este decât un caz degenerat al logicii adevărate, reale a
omului, Dominarea psihologică a ei ține de aceleași resorturi ca și dominarea
psihologică a geometriei euclidiene (pag. 360).
iar dacă
au apărut numai 10, resping fără șovăială aceeași ipoteză. Și totuși, am văzut
că din punct de vedere logic, orice asertare de limită este vidă de conținut
pentru șiruri date extensiv, fiind compatibilă cu orice segment inițial. Înseamnă
că logica noastră bivalentă este de vină și trebuie dată la o parte dacă nu
vrem să renunțăm la teoria probabilităților, transformând-o, prin renunțarea
la asertarea limitei într-o arhivă, o colecție stupidă de date fără valoare
predictivă. Și adevărul este că nici noi nu gândim după logica bivalentă, care
nu e decât o idealizare care se potrivește în mai multe cazuri tocmai pentru
că se neglijează latura probabilistă a cunoașterii (pag. 359). Credem că nu
se va putea lămuri niciodată problema adecvării teoriei probabilităților în
cadrul logicii clasice, căci în realitate, judecarea unei aserțiuni probabiliste
este ea însăți un demers probabilist (pag. 359). Trecerea la logica probabilistă,
este clar că Reichenbach nu o face ca un scop în sine: nu poate rezolva altfel
problema. Ea are caracterul saltului de la geometria euclidiană la cea riemanniană.
Logica clasică nu este decât un caz degenerat al logicii adevărate, reale a
omului, Dominarea psihologică a ei ține de aceleași resorturi ca și dominarea
psihologică a geometriei euclidiene (pag. 360).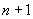 a oară
va apărea iarăși P) aplicată la frecvențe spune: dacă de n ori
observi frecvențele
a oară
va apărea iarăși P) aplicată la frecvențe spune: dacă de n ori
observi frecvențele  aproximativ
egale, inferă că tot așa va fi și a
aproximativ
egale, inferă că tot așa va fi și a  a oară.
Ea se bazează pe un pariu tacit al nostru: că lumea este previzibilă. În limbaj
probabilistic, că limita frecvenței există. Dacă este așa, regula inducției
ne va duce spre limită. Dacă nu, oricum ea este singura pe care o știm pentru
a prevedea. De aceea ea este justificată i se răspunde lui Hume. Un orb care
s-a rătăcit în munți, pipăie cu bastonul o cărare. El nu știe încotro duce această
cărare, nici dacă nu îl va arunca în prăpastie. Și totuși, în măsura în care
poate să o pipăie, el o va urma pas cu pas. Căci dacă pentru el există măcar
o posibilitate să ajungă undeva, aceasta este să-și pipăie în continuare cărarea.
În fața viitorului suntem ca acest orb; pipăim o cale (inducția n.n.) și știm:
dacă măcar un drum se poate găsi prin viitor, apoi acesta este de a pipăi în
continuare cu bastonul această cărare (pag. 420)
a oară.
Ea se bazează pe un pariu tacit al nostru: că lumea este previzibilă. În limbaj
probabilistic, că limita frecvenței există. Dacă este așa, regula inducției
ne va duce spre limită. Dacă nu, oricum ea este singura pe care o știm pentru
a prevedea. De aceea ea este justificată i se răspunde lui Hume. Un orb care
s-a rătăcit în munți, pipăie cu bastonul o cărare. El nu știe încotro duce această
cărare, nici dacă nu îl va arunca în prăpastie. Și totuși, în măsura în care
poate să o pipăie, el o va urma pas cu pas. Căci dacă pentru el există măcar
o posibilitate să ajungă undeva, aceasta este să-și pipăie în continuare cărarea.
În fața viitorului suntem ca acest orb; pipăim o cale (inducția n.n.) și știm:
dacă măcar un drum se poate găsi prin viitor, apoi acesta este de a pipăi în
continuare cu bastonul această cărare (pag. 420)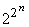 sunt
n libere) a căror
frecvență parțială tinde la
sunt
n libere) a căror
frecvență parțială tinde la 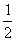 . Nu văd
cum se trece apoi la un p oarecare. În plus folosește noțiunea de frecvență
medie absolut liberă (pag. 196) pe care nu o definește, deși este esențială
pentru construcția pretinsă.
. Nu văd
cum se trece apoi la un p oarecare. În plus folosește noțiunea de frecvență
medie absolut liberă (pag. 196) pe care nu o definește, deși este esențială
pentru construcția pretinsă. . De ce
? Nu putem observa decât o serie finită, și în cadrul ei probabilitatea unei
succesiuni de 100 de steme, deși foarte mică, este totuși pozitivă. Speranța
că raritatea calculată a unui asemenea fenomen constituie un mijloc de falsificare
a estimării probabilistice se dovedește a fi iluzorie, întrucât orice apariție
frecventă a unor segmente lungi foarte divergente poate fi oricând considerată
ca nefiind altceva decât un segment mai lung și mai divergent pentru care sunt
valabile aceleași considerații: nu există nici un șir de evenimente determinat
extensional... care ar putea falsifica un enunț de probabilitate (pag. 199).
De aceea, ipotezele probabiliste ar trebui considerate ca neinformative din
punct de vedere empiric !
. De ce
? Nu putem observa decât o serie finită, și în cadrul ei probabilitatea unei
succesiuni de 100 de steme, deși foarte mică, este totuși pozitivă. Speranța
că raritatea calculată a unui asemenea fenomen constituie un mijloc de falsificare
a estimării probabilistice se dovedește a fi iluzorie, întrucât orice apariție
frecventă a unor segmente lungi foarte divergente poate fi oricând considerată
ca nefiind altceva decât un segment mai lung și mai divergent pentru care sunt
valabile aceleași considerații: nu există nici un șir de evenimente determinat
extensional... care ar putea falsifica un enunț de probabilitate (pag. 199).
De aceea, ipotezele probabiliste ar trebui considerate ca neinformative din
punct de vedere empiric ! -
un număr atât de mic, încât este imposibil de imaginat. Dar un asemenea fenomen
nu va putea apărea niciodată ca un efect fizic, deoarece datorită extremei
sal improbabilități el nu ar putea fi reprodductibil după voie. Chiar dacă un
fizician ar putea observa un asemenea proces, el ar fi incapabil să îl reproducă
și de aceea nu ar putea decide ce s-a întâmplat în realitate și dacă nu cumva
a făcut o eroare de observație. Dacă însă, abaterile de la un macroefect dedus
prin ipoteze probabiliste sunt reproductibile, presupunem că estimarea probabilistă
a fost falsificată.
-
un număr atât de mic, încât este imposibil de imaginat. Dar un asemenea fenomen
nu va putea apărea niciodată ca un efect fizic, deoarece datorită extremei
sal improbabilități el nu ar putea fi reprodductibil după voie. Chiar dacă un
fizician ar putea observa un asemenea proces, el ar fi incapabil să îl reproducă
și de aceea nu ar putea decide ce s-a întâmplat în realitate și dacă nu cumva
a făcut o eroare de observație. Dacă însă, abaterile de la un macroefect dedus
prin ipoteze probabiliste sunt reproductibile, presupunem că estimarea probabilistă
a fost falsificată. . Ca să
infirm această afirmație ar trebui să reproduc după voie o frecvență diferită
cu mult de
. Ca să
infirm această afirmație ar trebui să reproduc după voie o frecvență diferită
cu mult de 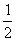 ? Nu
este o pretenție cam prea severă ? Dacă cineva aruncă un zar de 600 de ori și
nu apare nici un 6, el renunță fără nici o ezitare la ipoteza
? Nu
este o pretenție cam prea severă ? Dacă cineva aruncă un zar de 600 de ori și
nu apare nici un 6, el renunță fără nici o ezitare la ipoteza 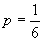 , fără
a considera necesar să mai reproducă efectul, fiindcă este convins că ceea ce
este prea puțin probabil nu se întâmplă, deși acest lucru i se pare iluyoriu
lui Popper. Și, în definitiv, de unde știu că un efect este reproductibil sau
nu ? Nu cumva se intră într-un cerc vicios respingând criteriul de falsificare
al improbabilității și înlocuindu-l cu cel de efect reproductibil ?
, fără
a considera necesar să mai reproducă efectul, fiindcă este convins că ceea ce
este prea puțin probabil nu se întâmplă, deși acest lucru i se pare iluyoriu
lui Popper. Și, în definitiv, de unde știu că un efect este reproductibil sau
nu ? Nu cumva se intră într-un cerc vicios respingând criteriul de falsificare
al improbabilității și înlocuindu-l cu cel de efect reproductibil ? la o
aruncare cu zarul ar însemna că rezultatul următoarei aruncări cu zarul ar fi
în mod obiectiv nedefinit și nedeterminat).
la o
aruncare cu zarul ar însemna că rezultatul următoarei aruncări cu zarul ar fi
în mod obiectiv nedefinit și nedeterminat).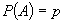 n.n.)
ci invers, probabilitatea unei ipoteze dacă evenimentul fixat se întâmplă
(§4.7a). Lucrurile se complică deoarece probabilitatea unei ipoteze nu mai are
interpretare frecvențială: ea este într-un grad și mai mare ipotetică, fiind
derivată prin regula lui Bayes sau prin metoda verosimilității maxime (regula
likelihoodului, care în cazul cel mai simplu, a două ipoteze h și h spune: dacă
n.n.)
ci invers, probabilitatea unei ipoteze dacă evenimentul fixat se întâmplă
(§4.7a). Lucrurile se complică deoarece probabilitatea unei ipoteze nu mai are
interpretare frecvențială: ea este într-un grad și mai mare ipotetică, fiind
derivată prin regula lui Bayes sau prin metoda verosimilității maxime (regula
likelihoodului, care în cazul cel mai simplu, a două ipoteze h și h spune: dacă  , acceptă
pe h). Prima regulă cere cunoașterea probabilităților apriori ale ipotezelor,
lucru foarte convențional și arbitrar; în schimb metoda a doua duce la rezultate
absurde, mai ales la eșantioane mici: de exemplu, dacă la o serie de trei aruncări
cu banul au apărut numai steme și dacă am aplica aniv regula verosimilității
am decreta că P(stemă) = 1 ! Pe lângă acaestă obiecție, mai
există un contraexemplu celebru (jocul cu bile al lui Ehrenfest) care arată
că metoda verosimilității ne duce la concluzii false. De aceea, Drieschner propune
următoarea metodologie de asignare a frecvenței relative prevăzute: Un eveniment
întotdeauna repetabil face în timp acea ipoteză mai probabilă care acordă
acestui eveniment, în ipotezele posibile, probabilitatea maximă (§4.7a). Cu
alte cuvinte, trebuie urmărit șirul
, acceptă
pe h). Prima regulă cere cunoașterea probabilităților apriori ale ipotezelor,
lucru foarte convențional și arbitrar; în schimb metoda a doua duce la rezultate
absurde, mai ales la eșantioane mici: de exemplu, dacă la o serie de trei aruncări
cu banul au apărut numai steme și dacă am aplica aniv regula verosimilității
am decreta că P(stemă) = 1 ! Pe lângă acaestă obiecție, mai
există un contraexemplu celebru (jocul cu bile al lui Ehrenfest) care arată
că metoda verosimilității ne duce la concluzii false. De aceea, Drieschner propune
următoarea metodologie de asignare a frecvenței relative prevăzute: Un eveniment
întotdeauna repetabil face în timp acea ipoteză mai probabilă care acordă
acestui eveniment, în ipotezele posibile, probabilitatea maximă (§4.7a). Cu
alte cuvinte, trebuie urmărit șirul  ;
;
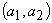 ;
;
 ;...;
;...;
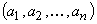 și căutată
acea probabilitate p pentru care această evoluție are probabilitatea
maximă. Este vorba de o modificare a metodei verosimilității, posibil (principial)
de aplicat cu ajutorul calculatoarelor.
și căutată
acea probabilitate p pentru care această evoluție are probabilitatea
maximă. Este vorba de o modificare a metodei verosimilității, posibil (principial)
de aplicat cu ajutorul calculatoarelor.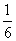 este
o proprietate fizică a zarului, ceea ce, evident nu se poate susține).
Este vorba numai despre o primă aproximație, necesară în abordări ulterioare:
În fizică, probabilitățile se vor aplica mai ales în aceste cazuri, adesea
cu ajutorul unor calcule din teoria grupurilor (§4.7b).
este
o proprietate fizică a zarului, ceea ce, evident nu se poate susține).
Este vorba numai despre o primă aproximație, necesară în abordări ulterioare:
În fizică, probabilitățile se vor aplica mai ales în aceste cazuri, adesea
cu ajutorul unor calcule din teoria grupurilor (§4.7b).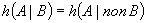 ), unde
h este frecvența relativă prevăzută; lucrul nu este posibil, stricto
sensu, decât dacă
), unde
h este frecvența relativă prevăzută; lucrul nu este posibil, stricto
sensu, decât dacă 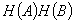 este
diviyibil prin N unde H înseamnă frecvența absolută, iar N
numărul probelor. Așa că definiția trebuie interpretată nuami aproximativ, eventual
folosindu-se funcția parte întreagă).
este
diviyibil prin N unde H înseamnă frecvența absolută, iar N
numărul probelor. Așa că definiția trebuie interpretată nuami aproximativ, eventual
folosindu-se funcția parte întreagă).